为什么模型可以从含噪声数据中学习到正确的信息?
很久没有认真记录自己的工作进展了。一方面是时间愈发紧张,另一方面也被各种日常琐事占据了精力。今天想借这个机会,简单介绍一下我们最近公开的一项研究成果。虽然说是“最新”工作,其实这项研究早在去年就已基本完成,只是最近才正式发布在 arXiv 上:
Why Can Accurate Models Be Learned from Inaccurate Annotations?
核心代码我们也开源了:
对我而言,做研究始终是兴趣驱动优先。这篇文章便是源于我很早之前就开始思考的一个问题:为什么模型在使用带有标注错误的数据训练时,仍然能够学习到正确的知识,甚至在某些场景下比用“干净标签”训练的模型表现还要更好?
在现实世界中,获取高质量、完美标注的数据往往成本高昂、困难重重。无论是因人为疏忽、领域歧义,还是主观判断的不可控性,不准确标注(inaccurate annotations)几乎无处不在。然而,与直觉相悖的是,大量实证研究表明:即使训练数据存在明显的标签错误,模型依然具备令人惊讶的“容噪能力”,能够从中提取出相对纯净的结构信息,完成精准预测。这种“明明喂了噪声,却能吐出真知”的悖论现象十分让人困惑,这也吸引了我们的研究兴趣,想要进行初步的探索。
实验观测
在开始之前,我们首先引入一个基本假设:模型在训练过程中所学习到的任务关键信息,通常以参数矩阵(尤其是分类权重矩阵)的形式被编码和存储。对于常见的深度学习分类模型而言,该参数矩阵对应于网络末端的全连接(Fully Connected, FC)层,其权重在训练中通过梯度优化所获得。我们用 $\mathbf{W}$ 表示在干净标签上训练得到的分类权重,而用 $\mathbf{W}'$ 表示在带有标注噪声的训练集上学到的权重。
其实,这个问题一开始让我们不知道该从哪里入手,像是长满了刺的刺猬,无从下口。但是,既然 $\mathbf{W}'$ 能够 work,我们猜测它和 $\mathbf{W}$ 之间可能有着某种关系。那么它们之间到底有多像?噪声到底影响了什么部分?
奇异值谱
我们做了一个系统性的实验:我们以 ResNet-34 作为 backbone,在 CIFAR-100 数据集的干净标签上进行训练,获得基准分类权重矩阵 $\mathbf{W}$ 。随后,我们引入不同程度的标签扰动,设定标签噪声概率 $p \in\{0.05, 0.1, 0.2, 0.3, 0.4\}$ ,得到每种噪声下的权重矩阵 $\mathbf{W}'$ 。然后我们分析了这些矩阵的奇异值——可以理解为模型“把信息压缩在哪些方向上”。我们发现:
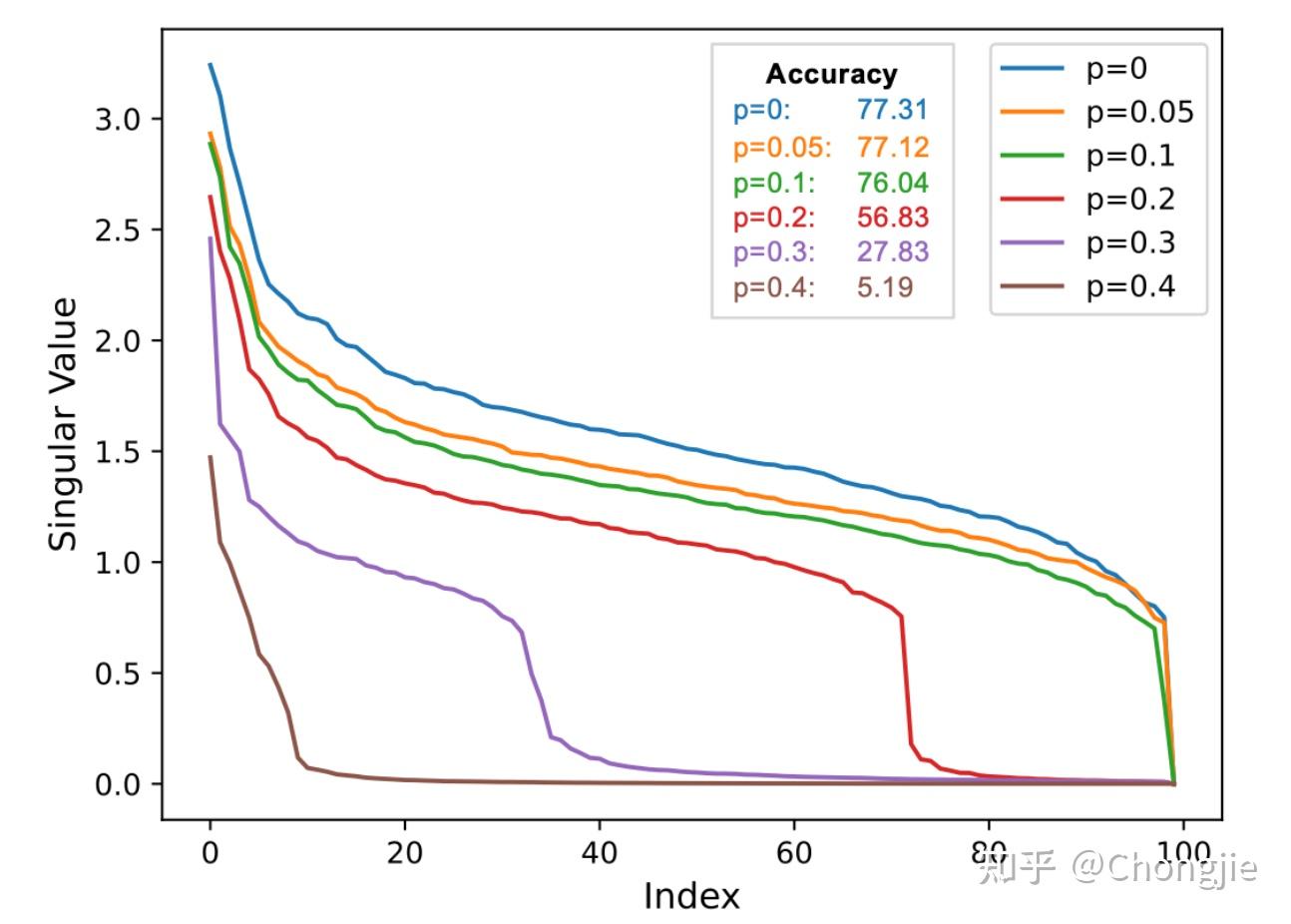
在标签不准确性处于较低水平(如 $p\leq 0.1$ )时, $\mathbf{W}'$ 的较大奇异值(即主奇异分量)与 $\mathbf{W}$ 几乎重合,说明主方向的信息保留完好,模型依然能够准确捕捉关键的分类判别特征。然而,当 $p$ 超过某一临界值后,这些主奇异值迅速衰减,模型权重开始失去沿主方向的有效信息积累,最终导致分类性能下降。同时我们还观察到,较大的标签噪声显著加快了奇异值的衰减速度,尤其是在尾部小奇异值处迅速接近零,意味着低秩方向受到了严重污染,进一步降低了模型的有效秩(effective rank)与鲁棒性。
这表明,标签不准确性一方面削弱了模型在主方向上的表示能力,另一方面通过积累干扰信息,加剧了权重矩阵的退化,最终影响整体分类性能。然而,尽管奇异值谱提供了整体退化趋势的宏观视角,我们仍然无法明确回答另一个关键问题:模型是否依然保留了关键的任务子空间结构?
子空间分析
为进一步解析这一问题,我们转向对奇异向量所张成的子空间结构进行对比分析。具体而言,我们比较由 $\mathbf{W}$ 的前 $i$ 个右奇异向量构成的主子空间 $\mathbf{V}_{:i}$ 与 $\mathbf{W}'$ 的前 $j$ 个奇异向量子空间 $\mathbf{V}'_{:j}$ 之间的相似性。我们采用基于 Grassmann 距离的归一化子空间相似性度量:
$$ \phi(\mathbf{V}, \mathbf{V}’, i, j) = \frac{\|\mathbf{V}_{:i}^{\mathsf{T}}\mathbf{V}’_{:j} \|_F^2}{\min (i,j)} \in [0,1], $$其中, $ \phi(\cdot) $ 的取值范围为 $[0,1] $ ,当取值为 1 时,表示两个子空间完全重合;取值为 0 则表示完全不相关。实验结果如下(为了偷懒我把图的caption也截了出来):
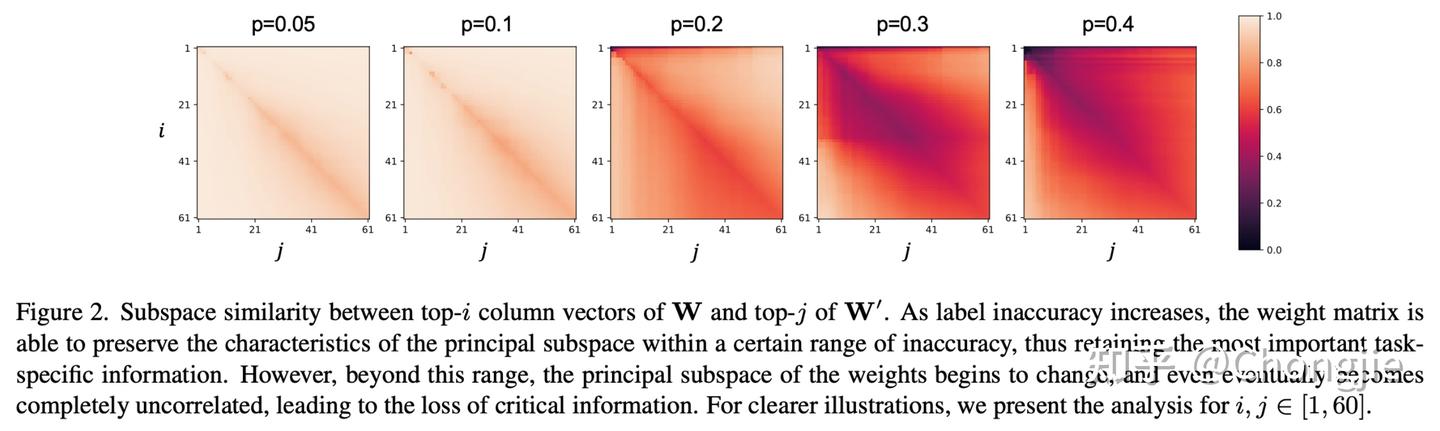
很明显,随着标签不准确性的增加, $\mathbf{V}$ 与 $\mathbf{V}'$ 所张成子空间之间的相似性整体下降,尤其在主子空间上最为明显。这说明主子空间的扰动与模型性能下降密切相关。换言之,标签噪声不仅破坏了低秩方向,也会在较高扰动水平下动摇模型的核心任务结构。另外但值得注意的是,当标签不准确性处于较低水平, $\mathbf{V}$ 与 $\mathbf{V}'$ 的主子空间相似性仍然维持在极高水平,甚至几乎重合,说明 $\mathbf{W}'$ 尽管源自带噪标签,但其任务相关的信息子空间结构仍然被完整保留。我们进一步验证发现,此时模型的分类精度与使用干净标签训练的模型几乎无差别,进一步支持了我们的判断:模型之所以能从不准确标注中学习到正确信息,是因为其分类权重矩阵在主子空间上仍保持高度一致。
好了,到这,我们似乎已逐步接近问题的核心。但若要真正把握其本质,仍需回答一个关键问题:为何在一定范围内,标签噪声并不会扰动分类权重的主子空间?
理论证明
理论证明的过程嘛,说实话,通常都不太有趣。大段的数学公式读起来确实有点枯燥。
我还记得自己刚开始接触科研那会儿,做的是比较“经典”的机器学习。每次看到一篇论文里铺天盖地的公式,第一反应就是头有点大。不是因为不懂(其实我一直挺喜欢数学的),而是因为心里隐隐会犯嘀咕:这些内容真的有那么重要吗?我是不是要花很多时间去理解一件最终可能并不影响我实验结果的事?
比如 ADMM(交替方向乘子法)这种优化方法,虽然理论上挺漂亮,但我真正用起来的时候,往往只是改几行代码参数而已,根本没必要把每一个凸优化的步骤都推导一遍。于是,渐渐地我也学会了“适可而止”地看理论——必要时吃透它,不必要时放过自己。
当然,这也影响了我后面写带有数学证明的论文风格:如果能讲得轻松一点,我绝不会故作深沉;如果一段推导真的没啥新意,我也愿意直接告诉你结论:
$$ \sin\theta \leq \frac{\sigma_{\max}(\mathbf{X}) \sqrt{nl}}{\delta(\lambda_{\min}(\mathbf{X}^\mathsf{T}\mathbf{X}) + \lambda)} \sqrt{p}. $$这里解释一下两个参数: $\theta$ 是受噪声扰动前后主子空间的夹角(即 $\mathbf{W}$ 和 $\mathbf{W}'$ 主子空间的夹角), $p$ 是数据的噪声程度。其他的参数都可以视作超参数(不过还是解释一下, $\mathbf{X},n,l$ 分别是样本矩阵、样本数、标签数, $\lambda_{\min}(\cdot)$ 表示矩阵最小的特征值, $\lambda$ 是正则项的系数, $\delta$ 就看成是一个超参数吧)。感兴趣的读者可以参考原论文的推理过程。
我们用理论进一步验证了这一点:主子空间之间的夹角变化非常小,意味着这部分信息结构在带噪声的数据下依然保持稳定。正是这种稳定性,让模型具备了“在噪声中学习真知”的能力。我们最终得出了一个非常关键的结论:
只要标签的不准确程度还在一个合理范围内,模型学到的“主子空间”——也就是承载主要任务信息的那部分权重结构——几乎不会发生太大的变化。
LIP
到这里,我想我们对这一问题的探索先告一段落。不过可能有人会问,上面这些分析能不能带来更加 practical 的作用?
当然是可以的。
经过前面的实证观察和理论分析,我们发现:只要标签不准确的程度不太夸张,模型的核心“知识结构”——也就是权重矩阵的主子空间——并不会受到太大影响。真正的问题在于:标签错误会在一些“靠后的奇异方向”引入噪声,干扰模型表现。
那有没有办法,在不改动模型的情况下,把噪声过滤掉,只保留最有用的信息?
我们设计了一个非常简单但效果显著的小模块,叫做 LIP(Label Inaccuracy Processor)。它不是新的模型结构,也不是一个新的训练范式,而是一个轻量的后处理插件(plug-in),可以直接接入任何已有模型,实现“稳住主方向,修复细节噪声”。
LIP 总共分两步:
主子空间保持(PSP)
我们首先对分类权重矩阵做奇异值分解(SVD),提取出最前面的 $k$ 个奇异值和对应的奇异向量——这些部分正是模型在训练中“记住”的最核心任务信息。我们用这些信息构建一个新的矩阵 $\mathbf{W}_k$ ,它代表了模型在干净任务上的“主干知识”。公式如下:
$$ \mathbf{W}_k = \mathbf{U}_k\mathbf{\Sigma}_k\mathbf{V}_k^{\mathsf{T}}. $$其中, $ \mathbf{U}_k, \mathbf{\Sigma}_k, \mathbf{V}_k $ 都表示前 $k$ 个分量。这一部分操作,就像是在说:“这些是模型真的学会的东西,先锁住不动。”
标签模糊度修复(LAP)
但我们并不满足于此。很多过去的工作都提醒我们:那些低奇异值部分可能不只是噪声,它们也可能包含一些重要的细节知识,尤其是在多样性更强、任务更复杂的场景中。标签不准确往往使这些尾部奇异值呈现扁平化、趋近于零的状态,这说明标签噪声在显著抑制这些成分的有效性。
基于上述观察,我们认为这部分被认为是“噪声”的尾部奇异值中,可能隐藏着被误伤的有用信息。因此,我们不是简单地将其舍弃,而是尝试对其进行修复和重估,以期从训练数据中重新提取关键特征,并提升整个权重矩阵的有效秩(effective rank)。于是我们重新训练这些奇异值。我们设定一个简单的优化目标,让这部分信息尽可能重建训练数据中的真实标签。
简单来说,我们令 $ \mathbf{U}_l, \mathbf{\Sigma}_l, \mathbf{V}_l $ 分别表示剩下的奇异分量(即step1中没有用到的)。权重可以表示成:
$$ \mathbf{W}’ = \mathbf{W}_k + \mathbf{U}_{l} \mathbf{\Sigma}_{l} \mathbf{V}_{l}^{\mathsf{T}}. $$为了重建尾部奇异值 $ \mathbf{\Sigma}_l $ ,我们在保持 $ \mathbf{U}_l $ 和 $ \mathbf{V}_l $ 不变的条件下,通过最小化分类误差,重新学习 $ \mathbf{\Sigma}_l$ 中的参数。具体优化目标如下:
$$ \min_{\mathbf{\Sigma}_{l}} \|\mathbf{X}\mathbf{W}’ - \mathbf{Y}\|_{F}^2 $$即,从原训练数据中重新学习奇异值。更重要的是——这个优化有闭式解!换句话说,整个过程完全不需要反向传播,也不需要再训练一轮模型。他的解为:
$$ \mathbf{\Sigma}_{l}^{*} = \frac{\mathrm{diag}(\mathbf{U}_l^\mathsf{T} \mathbf{X}^\mathsf{T} (\mathbf{Y} - \mathbf{X} \mathbf{W}_k) \mathbf{V}_l)}{\mathrm{diag}(\mathbf{U}_l^\mathsf{T} \mathbf{X}^\mathsf{T} \mathbf{X} \mathbf{U}_l)}. $$如此,我们便形成了 LIP 这一轻量化的插件。说他是轻量化,到底有多轻量?在 CIFAR-100 和 CUB-200 这两个数据集上,LIP 只需要 10ms 左右。
我们再来看看效果:
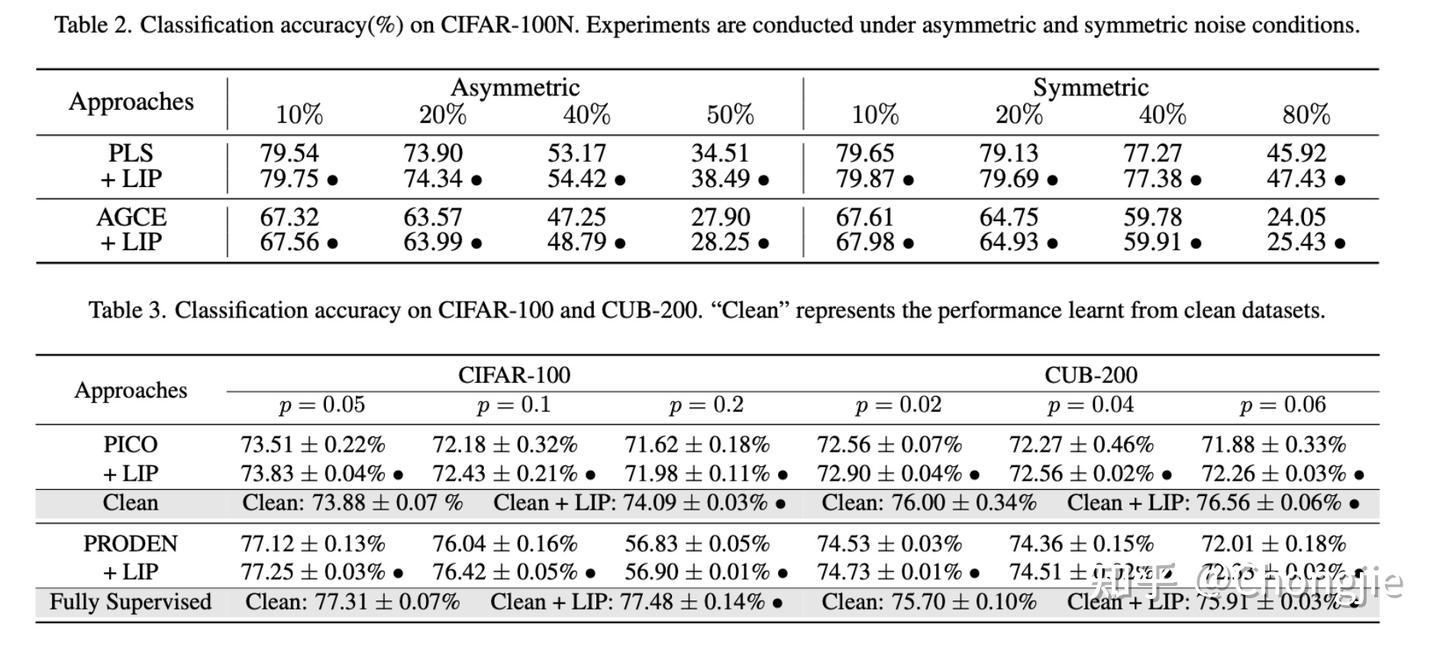
反正是一个不费时不消耗资源的插件,插上后性能还都有提升,何乐而不为呢(🐶)
关于更多细节与内容,欢迎参考我们的原论文。