模型融合的系数到底应该是多少?
今天给大家继续介绍我们的一个比较有趣的工作。
NAN: A Training-Free Solution to Coefficient Estimation in Model Merging
在开始之前先给这个工作补充些背景知识。
随着多任务模型在各类应用中越来越常见,预训练模型在 NLP 和 CV 领域的使用也变得非常普遍。现在我们只需要在下游任务上做一点点微调,就能取得不错的效果,这大大提高了开发效率。像 HuggingFace Transformers、timm、torchvision 这些平台也非常活跃,各种 backbone 和下游模型一应俱全。
但问题也来了:每个任务都保存一个独立模型,模型数量一多,存储压力和部署成本就跟着上来了,尤其是系统需要同时支持多个任务的时候,这种做法就显得非常不划算了。
于是,模型融合(Model Merging)开始被越来越多的人关注。它的思路其实挺简单的:能不能把多个任务已经微调好的模型“合并”起来,既保留它们各自的能力,又省下模型数量带来的开销?这个方向听起来很有吸引力,不需要原始训练数据,也不用重新训练多任务模型,做法轻量,应用灵活,确实挺有前景的。
不过,说起来简单,做起来还真有不少挑战。
其中最关键的一个问题就是:模型怎么合?
大家现在常用的方法,大多是把两个模型的权重做某种“平均”——比如简单加权平均、插值或者做一些任务向量方向上的操作。但这里面有个隐藏的大坑:这个“加多少”“乘多少”的系数到底怎么设?很多方法其实都是靠直觉,比如“我们感觉这个任务更重要,所以给它多加点权重”,或者“我们试了几个数字,哪个效果好就用哪个”。虽然有时候能跑得通,但这种方式不够稳,也很难推广到更复杂的任务组合里。尤其当不同模型之间存在结构差异或性能差距的时候,盲目加权很容易把一个本来挺好的模型给“拉垮”了。
为了让大家更直观地理解这个“系数怎么设”的问题,我们来看看两个比较典型的例子:
首先是 Task Arithmetic。它的融合方式很简单粗暴:两组模型参数直接做线性插值,然后……就用 0.3 作为融合系数。不是 0.5,也没有动态计算,就是 0.3。为什么是 0.3 ?没有特别说明。这其实就是一种典型的“拍脑袋”式经验设定——在某些任务上也许能凑效,但显然缺乏普适性和解释性。
再来看 AdaMerging,它尝试做得更精细:通过引入监督信号,训练出一组layer-wise 的融合系数。下面这张图展示的是在融合 8 个模型时,不同层的权重(共 156 个)所学习到的系数分布:

可以看到,每层的参数都拥有不同的融合权重,这确实更精细了。但问题也来了:这样的做法虽然效果好,但训练成本高,步骤复杂,而且往往需要针对每个新任务重新学习一遍。也就是说,它不够轻量,也不够通用。
所以不难看出,无论是 Task Arithmetic 的“一刀切”,还是 AdaMerging 的“量身定制”,目前的融合系数设计仍处于两个极端之间徘徊:
要么太粗,要么太重。我们还缺少一种既自动、又可解释,还能稳定泛化的方法,真正把模型融合这件事变得“即插即用”。
好的,介绍到这里,想必读者朋友们也差不多猜到我们想干什么了:我们希望找到一种既不靠拍脑袋、又不需要重新训练的融合系数确定方法,让模型融合真正做到高效、可控、通用。
这件事说起来轻松简单,但是要从哪里开始入手呢?
我们转了一圈,决定从最基础、最朴素、也最讲道理的一个角度出发——最小二乘(least squares)。没错,这个经典得不能再经典的优化问题,其实可以帮我们重新理解“模型融合”到底是怎么回事,甚至还顺带告诉我们:你到底该怎么选融合系数。
从最小二乘出发,模型融合还能这么看?
先假设我们有两个任务,给定彼此的数据集,我们使用最小二乘损失作为优化目标:
$$ \min_{\mathbf{W}_1} \|\mathbf{X}_1 \mathbf{W}_1 - \mathbf{Y}_1\|_F^2, \quad \min_{\mathbf{W}_2} \|\mathbf{X}_2 \mathbf{W}_2 - \mathbf{Y}_2\|_F^2, $$每个任务都训练出了自己的模型( $\mathbf{W}_1$ 和 $\mathbf{W}_2$ ,都有对应的闭式解),那问题来了——我们现在想合成一个“通吃”的模型 $\mathbf{W}^*$ ,它能在两个任务上都表现不错。我们把这件事转成数学语言:两个模型原本各自是通过最小化自己的误差学出来的,那我们就试试看,把两个任务的误差加在一起,然后再最小化:
$$\mathbf{W}^* = \arg\min_{\mathbf{W}} \|\mathbf{X}_1 \mathbf{W} - \mathbf{Y}_1\|_F^2 + \|\mathbf{X}_2 \mathbf{W} - \mathbf{Y}_2\|_F^2$$如此,我们便可得出 $\mathbf{W}^*$ 的闭式解。接着,通过一些简单的数学代换,我们便可以用 $\mathbf{W}_1$ 和 $\mathbf{W}_2$ 来表示 $\mathbf{W}^*$ :
$$ \mathbf{W}^* = (\mathbf{X}_1^\mathsf{T} \mathbf{X}_1 + \mathbf{X}_2^\mathsf{T} \mathbf{X}_2)^{-1}\mathbf{X}_1^\mathsf{T} \mathbf{X}_1\mathbf{W}_1 + (\mathbf{X}_1^\mathsf{T} \mathbf{X}_1 + \mathbf{X}_2^\mathsf{T} \mathbf{X}_2)^{-1}\mathbf{X}_2^\mathsf{T} \mathbf{X}_2 \mathbf{W}_2 $$这么看似乎不直观,我们用分式的形式做一步不那么正规的变换:
$$ \mathbf{W}^* = \frac{\mathbf{X}_1^\mathsf{T} \mathbf{X}_1}{\mathbf{X}_1^\mathsf{T} \mathbf{X}_1 + \mathbf{X}_2^\mathsf{T} \mathbf{X}_2}\mathbf{W}_1 + \frac{\mathbf{X}_2^\mathsf{T} \mathbf{X}_2}{\mathbf{X}_1^\mathsf{T} \mathbf{X}_1 + \mathbf{X}_2^\mathsf{T} \mathbf{X}_2}\mathbf{W}_2$$看上去顺眼多了,我们再变换一下:
$$ \mathbf{W}^* = \frac{a}{a+b}\mathbf{W}_1 + \frac{b}{a+b}\mathbf{W}_2 $$到这里,是不是就能很轻松地看出,模型融合是一种“加权融合”。“加权平均”两个模型,权重不是 0.3,也不是 0.5,而是和每个模型输入特征的“信息量”有关。具体点说,那些输入特征变化大、分布广的任务,就应该在合并时占更多比重。我们用的是特征协方差矩阵(没错,就是 $\mathbf{X}^\mathsf{T}\mathbf{}$ )来量化信息量,这样得出的融合结果更合理,也更稳。
但是,我们还不满意,因为此时的融合系数还涉及到训练的数据。我们能不能把这个也规避了?
协方差的一种替代方式
如果你平时做模型训练,一定知道大家习惯把特征先归一化。这个时候,特征的协方差矩阵其实就和样本数差不多成正比了。于是我们发现——
- 如果每个模型的输入都差不多归一化过,那最佳的融合权重,其实就该和每个模型训练用的数据量成比例。
这个结论超级直观,也很好理解:谁用的数据多,谁学到的信息就多,那自然也应该在合并的时候多说点话。
听起来不错,但问题来了:大部分时候,我们还是不知道这些模型具体是在哪儿、用了多少数据训练出来的。模型是开源的,参数能拿到,训练细节却很难还原。
怎么办?我们绕开数据量,直接去看模型本身:有没有什么信号能反映数据量?答案是——参数的方差。
我们翻阅了一些研究,发现其中有一些结论:一个模型如果训练数据多,那它学出来的参数更新会更稳,也就是说,参数之间不会乱跳,方差小;而数据少的模型,学出来的参数就比较“飘”。于是我们就用参数的方差,来当作训练样本量的一个代理。再简化一下:既然模型的参数大多是零均值,我们就可以用 Frobenius 范数来代替方差了。
至此,一个简单的 training-free 的融合方法 NAN(Norm-Aware Merging)就呼之欲出了,一个不需要任何训练、拿来就能用的模型融合小插件。它的做法非常简单:
- 取出每个模型的参数;
- 计算它们的范数;
- 用范数的倒数做归一化,就得到了融合系数。
更多的细节还请参考原论文。
来看看效果。我们分别展示 CV、NLP 和 MM 的效果。
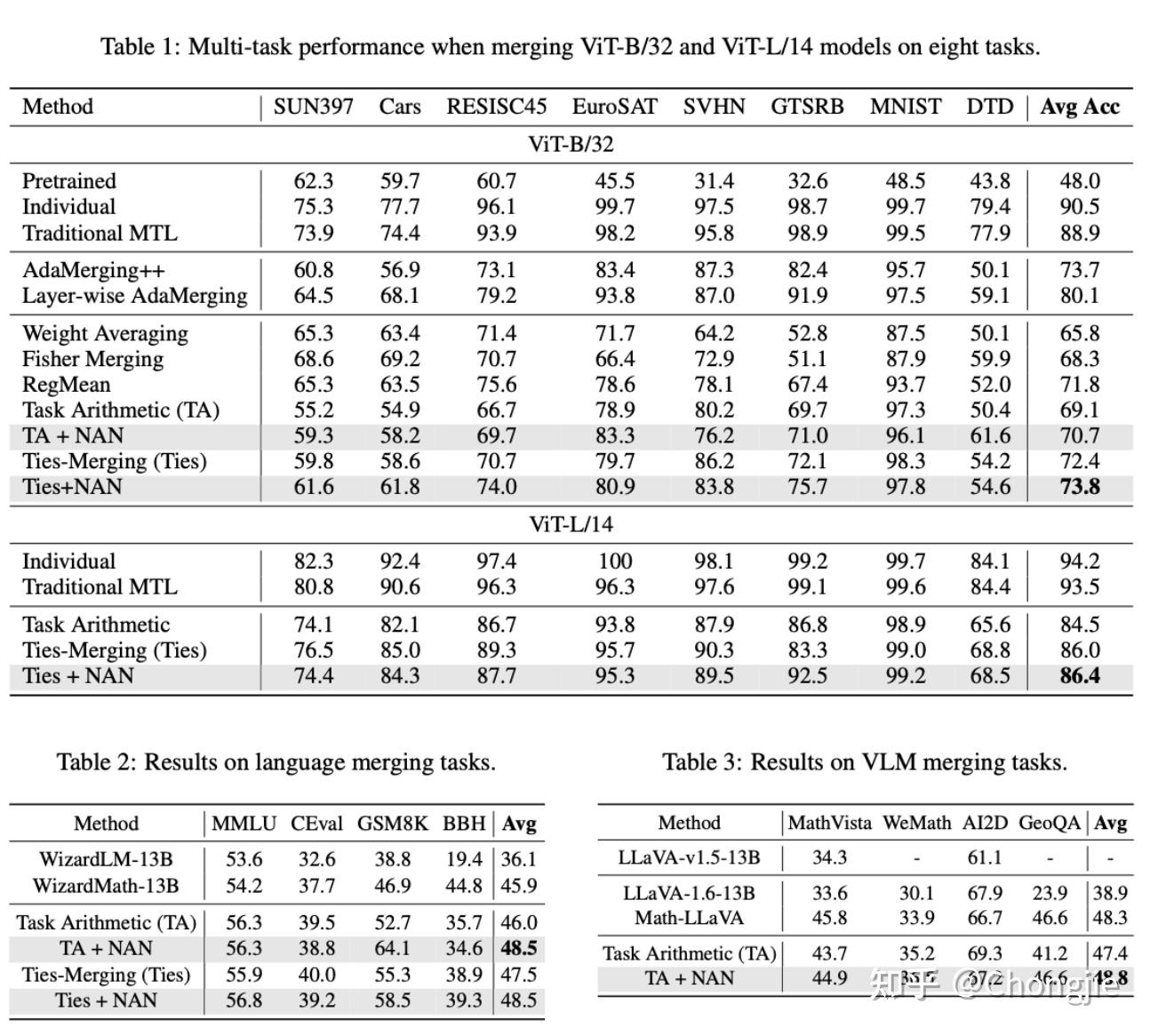
效果感觉害行。
其他一些趣事儿
说到这,其实还有点幕后小故事可以分享。
这个工作啊,其实很早就搞完了,核心思路、公式推导、实验代码都在。但是呢,就差最后一步:动手写。于是它就这么在文件夹里静静躺了好几个月,被我们拖着、忘着、搁着。
直到我快要离职了,直到某个会议截稿前两天,我突然决定,把这个写成论文。当时的想法特别简单——当个小品文乐一下,把它当作科研生活的一个段子收个尾,也算没白忙活。
反正实验数据都在,代码也不需要动,唯一的任务就是写。于是我花了一个下午写完了这篇论文(也就是目前arXiv上挂着的这一版本),交给了老师。然后就submit了。
巧的是,那几天正好是 rebuttal 高强度回邮件的时期。老师在忙别的论文,直到第二天晚上,那边才刚准备和我“正式讨论一下这个工作”。
我说:老师,ddl过了。
老师:???我擦,啥时候
我:刚刚
还有个有趣的插曲,其实这个项目最早的时候,我们的思路是从没有 pre-trained model 出发的。当时大多数融合方法本质上都是在算 fine-tune 后的模型减去 pre-train 的模型,然后再对这个“差值”进行融合。说白了,pre-train 是默认必须要知道的,甚至要参与计算。但我们就想了个问题。有没有可能,不依赖 pre-trained 模型,直接融合 fine-tuned 结果?再深一层,由于我们加权的时候不知道要融合的模型是 sft 的还是 pre-trained,有没有什么更公平的无偏的融合方式?
我们很快想出来一个做法。然后,我们很快把它否了,因为太简单了(笑)。于是我们就转头做了现在这个更 general、更理论驱动的 NAN。
最神奇的是,就在这篇论文刚写完那几天,突然刷到了一篇新文章,是字节的工作:Model Merging in Pre-training of Large Language Models。我们点进去一看,发现他们的做法居然和我们最开始那个被我们自己否掉的方案非常像。
不过也确实不完全一样——我们当时是用在下游的 SFT(supervised fine-tuning),他们是在更早期的 pre-training 阶段做的。方向接近,目标不同,也算是种“学术撞思路”吧。
所以当即立刻,我们就把这篇论文挂出来了。