李群视角解决N维参数的高效微调
在之前的工作中,我们提出了现有的参数高效微调的一个关键问题:
多数低秩微调策略(如 LoRA、DoRA、MoRA、AdaLoRA 等)主要针对线性层和嵌入层等二维张量设计,难以有效扩展至卷积等高维张量结构。尽管可以通过 reshape 操作将高维参数展开为二维形式以适配这些方法,但此举不仅破坏了卷积核的结构归纳偏置,还在维度升高时导致参数激增,违背了微调方法的高效性初衷。
在上个工作里,我们提出了 FLoRA,一种面向高维张量的全局低秩微调框架。FLoRA 通过引入统一的低秩核心空间,实现对各维度参数的协同建模与微调,在保留张量原始拓扑结构与维度间交互性的同时,显著提升了高维神经算子的适应能力和参数利用效率。
然而,上述设计仍面临几个核心问题:
- 卷积结构在主流模型架构中的使用正逐渐减少,当前的主流仍是以 Transformer 为代表的全连接线性结构,因此专门为卷积等高维张量设计的微调机制,其适用范围相对有限。
- 在二维场景中,FLoRA 仍采用低秩更新方式,未能在结构上实现满秩的自由度调控,其空间结构保持能力仍受限。
最关键的是,当前已有的大量微调方法已高度成熟并被广泛应用于线性模块中,因此一个更具普适性的研究方向是:
- 能否充分利用现有线性方法的繁荣发展,直接利用这些方法构建一种适用于任意维度张量的结构保持机制,使线性低秩策略在更复杂的张量空间中依然具备表达能力和结构对齐性?
这不仅有望统一当前分裂的高低维微调方案,也为未来模型架构的兼容性提供更通用的解决方案。
读到这里,想必读者已经知道我们这个工作是想做什么了。
Generalized Tensor-based Parameter-Efficient Fine-Tuning via Lie Group Transformations
这一工作目前发表于 2025 ICCV。
将权重视作李群元素
在开始之间,我们先简单介绍一下大概的思路:
我们首先基于这样一个观察:微调后权重的改变量通常都非常小而且不为零,因此可以把它们看成对预训练权重的微小扰动。在这种情况下,所有这些参数就像是一个光滑流形上的点。如果我们给这个空间定义一个合适的群乘法运算,就能把它们当作李群的元素来看待。在这个框架下,我们把微小的扰动视作对应的李代数中的向量——在那里,你可以像平常一样做加法和数乘。接着,利用指数映射的局部微分同胚性质,我们把李代数里的更新“平滑地”映射回李群,从而在保持原有结构相关性的同时完成参数更新。
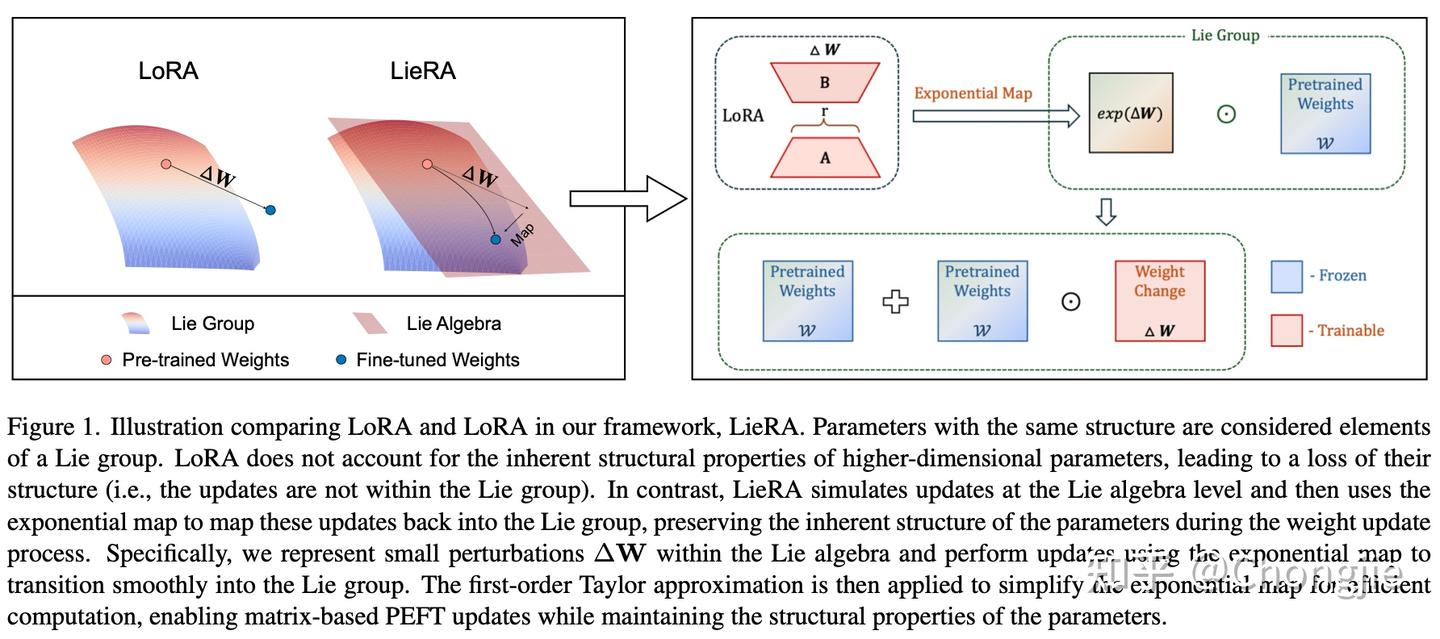
OK,看到这里读者可能觉得一头雾水,接下来我们一点点的进行分析。
构建李群
首先,我们构建一个高阶张量的集合。为了方便,我们可以将阶数定义为4,这么一来,我们可以将集合内任意的元素看作是一个卷积核的参数。定义 $G = \Big\{\mathcal{W} \in \mathbb{R}^{C_{\mathrm{in}} \times C_{\mathrm{out}} \times k \times k} \,\Big|\, W_{c,i,j,l} \neq 0,\; \forall\, c,i,j,l \Big\}$ 。考虑到实际情况与计算机精度的问题,我们对集合还额外施加了元素非0的条件。如果能找到一个合适的算子,那么这个集合就可以构成一个群。还是为了简单,我们可以选择 Hadamard 积作为这一算子,即“群乘法” $\circ$ 。这样:
- 相乘后仍然不会出现零元素,闭包性 OK;
- 乘法可交换,满足结合律;
- 全 1 张量是单位元;
- 每个张量都能做“倒数”变成它的逆元。
所以, $(G,\circ)$ 完全满足群的条件。更进一步,而且因为它本质上是很多个一维“去掉零点的实数”组装而成,还天生就是一个阿贝尔群,又是一个光滑流形,因此,他也是一个李群。
李群,李代数,李括号
讲完了李群,自然而然少不了对应的几个名词:李代数和李括号。我这里先不介绍他们具体的定义,而是用一个形象的比喻让读者更加直观的感受到他们之间的关系。
- 李群 ≈ 圆球(地球):想象你站在地球(一个球面)上,每个点对应一个卷积核参数配置。地球表面就是我们的李群,每个位置都有自己的坐标,但你只能沿着地球表面移动——这就是群里定义的“合法操作”(乘法运算)保证你始终留在群里。
- 李代数 ≈ 切线平面:在地球某一点上,你可以画一张“切线平面”——这是一块与地球表面只在一点相切的小平面。这个平面就是李代数,里面是线性的,你可以自由地在平面上画直线、做加法、数乘。
- 李括号 ≈ 两次不同方向的小路差异:如果你先在切线平面上走一小段向量 $\mathbf{X}$ ,再走一小段向量 $\mathbf{Y}$ ,然后反过来先走 $\mathbf{Y}$ 再走 $\mathbf{X}$ ,这两条路最终会在球面上有微小的偏差。李括号 $[\mathbf{X},\mathbf{Y}]$ 就是用来衡量这种“走 $\mathbf{X}\rightarrow \mathbf{Y}$ ” 和 “走 $\mathbf{Y}\rightarrow\mathbf{X}$ ” 顺序差异的张量。在阿贝尔(交换)李群里,这个偏差正好是零——也就是说,不管先后顺序,结果都一样。
通过这个“地球—切平面—走路—回表面”的比喻,我们就能直观地理解:
- 李群是我们想要留在上面的曲面;
- 李代数是让更新变得简单的平面;
- 李括号则是衡量“换个顺序走路”有没有影响。
好的,那么说完这些,再回头看我们构造的李群。对这个群来说,李代数就是把每个卷积核张量看作普通的实数张量,在线性空间里做加法和数乘就行,完全和我们平时在 PyTorch 里对张量做操作一样。因为群是阿贝尔的,李括号对任何两个元素都给 0,不用管。我们已经把卷积核参数看成了李群 $G$ 中的元素,而在这个群里直接做更新其实相对繁琐(需要不断地“乘法+求逆”等操作),不如把更新“放到”对应的李代数 $\mathfrak{g}$ ——一个熟悉的线性张量空间里,一切像在 PyTorch 里那样直接做加法和数乘。
如何在李代数上更新
对于任意一个卷积核 $\mathcal W\in G$ ,我们先不动它,而是构造一个小扰动 $ \Delta\mathcal W\in\mathfrak{g}$ 。在这里, $ \Delta\mathcal W$ 就是一个普通张量——你用 .grad、.add_()、.mul_() 以及 reshape(如此便可以纳入针对二维空间的方法)都能直接操作。完成了线性更新后,我们需要把扰动“平滑地”带回李群 $ G $ ——否则 $ \mathcal W \circ\Delta\mathcal W$ 并不一定留在群里。指数映射 $ \exp:\mathfrak{g}\to G $ 就是专门干这件事的“桥梁”:
- 局部同胚:保证极小扰动在映射后还能保持连续、不跳出合法空间;
- 结构保留:映射后 $ \exp(\Delta\mathcal{W}) $ 还是在群里,对应位置上是指数缩放,比例更新不破坏卷积核的“形状”;
- 几何一致:更新结果能沿着群流形上的自然方向变化,不像任意加法那样随意。
更新公式因此变成了
$$ \mathcal W \;\mapsto\; \mathcal W \;\odot\; \exp\bigl(\Delta\mathcal W\bigr) $$既保留了群运算的合法性,也享受了李代数线性优化的便捷。但这还不够:尽管指数映射这么强大,但直接计算逐元素 $\exp$ 也有点小开销。好在我们的 $\Delta\mathcal W$ 本来就设计得足够小,于是可以用一阶泰勒快速近似:
$$ \exp(\Delta\mathcal W) = \mathcal I + \Delta\mathcal W + o\bigl(\|\Delta\mathcal W\|\bigr) \;\approx\; \mathcal I + \Delta\mathcal W$$带入主更新公式就得到:
$$ \mathcal W \odot (\mathcal I + \Delta\mathcal W) = \mathcal W + \mathcal W \odot \Delta\mathcal W $$这样,我们只多做了一次 Hadamard 乘法,就能近似实现李群意义下的指数更新。
对于二维空间来说,这种更新方式可以保持满秩。更多细节请看论文。
实验效果
我们先展示在高维张量上的效果
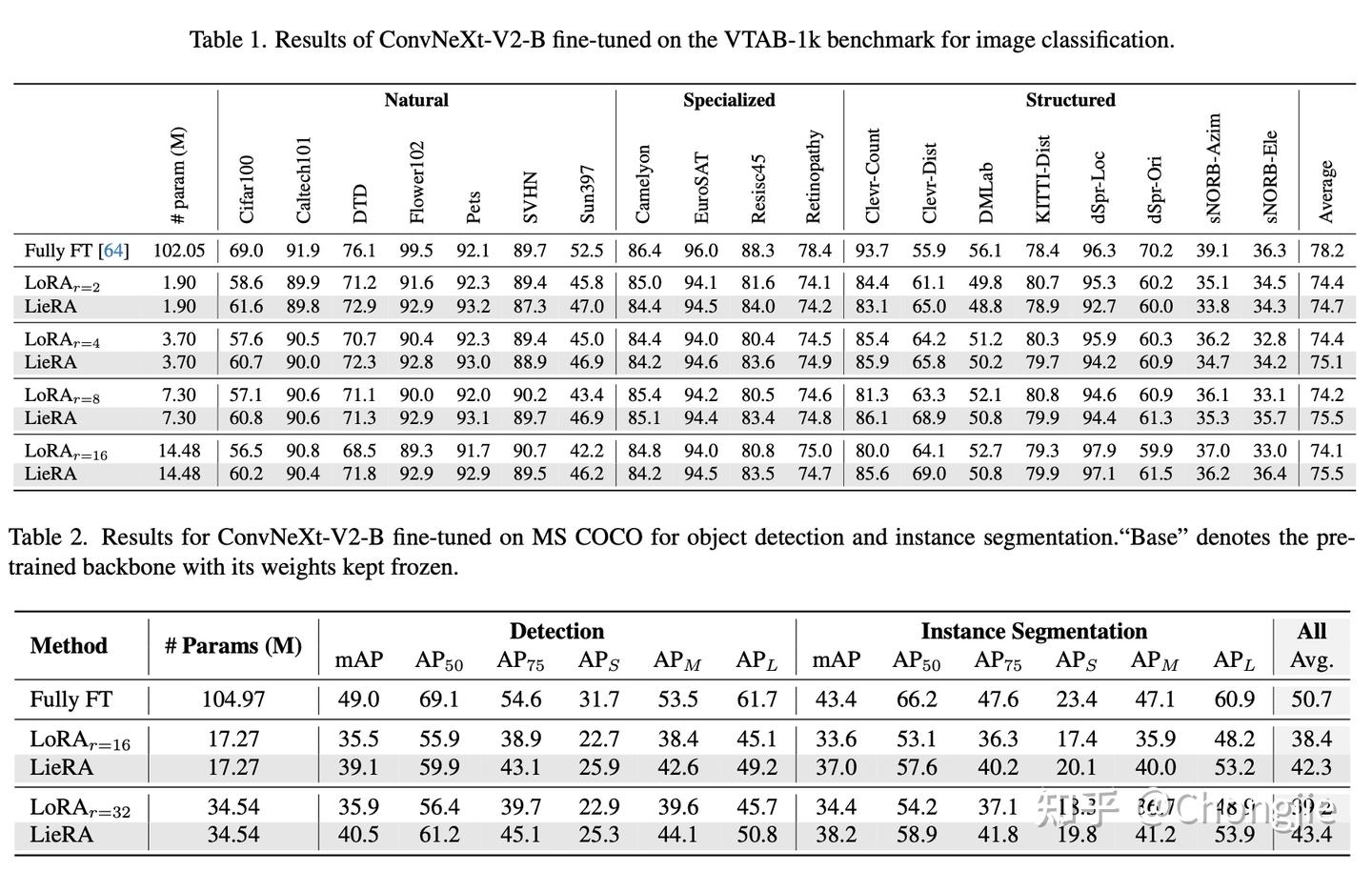
可以发现,在更复杂的检测和分割上,我们的方法效果还是比较明显的。对于以二维矩阵参数为主的任务,我们也进行了测试:
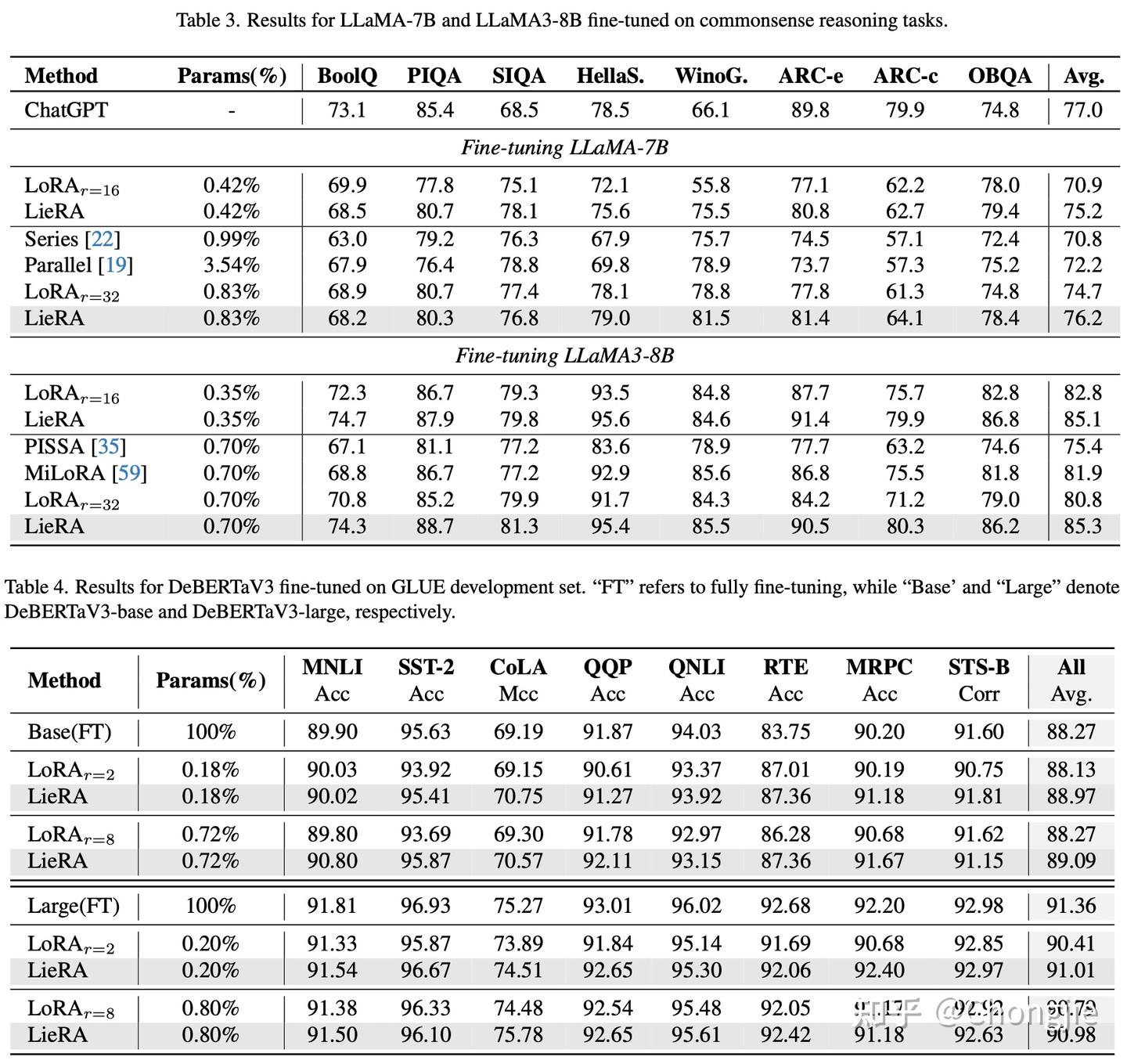
关于更多细节与内容,欢迎参考我们的原论文。