漫谈LoRA
我第一次了解到 LoRA 并非通过阅读学术论文,而是通过口耳相传。当时,我只是模糊地知道 LoRA 涉及模拟权重的变化。后来,我终于阅读了 LoRA 的论文,遗憾的是,第一次阅读时并没有看完整篇文章,只大致了解了该方法的实施细节和效果。我相信很多人在阅读学术论文时可能也有类似的操作,哈哈。
随着我对参数高效微调领域的深入学习,我发现一个非常有趣的现象:自 LoRA 提出以来已经过去了几年,现今的研究仍常以 LoRA 作为基准进行比较。这一点与一个热门领域的常规做法似乎有些矛盾。于是我开始重新阅读 LoRA 的论文,这一读便是反反复复快一年时间。不夸张地说,即便到今天,我仍然在反复学习这篇论文。虽然其内容已定,但每次阅读后我都能产生新的想法,每次都有新的收获。
以下是 LoRA 的做法:
LoRA 的做法实际上非常简洁。它并未直接对预训练的权重 $\mathbf{W}\in\mathbb{R}^{n\times m}$ 进行修改或训练新的权重,而是专注于学习从预训练权重到下游任务过程中的权重变化 $\Delta\mathbf{W}\in\mathbb{R}^{n\times m}$ 。为了提高参数效率,LoRA 采用了低秩表示法,认为 $\Delta\mathbf{W}$ 可以通过两个低秩矩阵的乘积来表示,即 $\Delta\mathbf{W}$ 可以分解为矩阵 $\mathbf{A}\in\mathbb{R}^{n\times r}$ 和 $\mathbf{B}\in\mathbb{R}^{r\times m}$ 的乘积。在训练阶段,LoRA 仅对矩阵 $\mathbf{A}$ 和 $\mathbf{B}$ 进行更新,同时保持预训练的权重 $\mathbf{W}$ 固定不变。在测试阶段,LoRA 将训练得到的 $\Delta\mathbf{W}$ 与预训练权重 $\mathbf{W}$ 结合,因此不会引入额外的计算损失。
至此,我们已经完成了对 LoRA 的基本介绍。然而,仅仅进行简单的分析,就能发现还有许多问题亟待解决:
- $\mathbf{A}$ 和 $\mathbf{B}$ 的初始化。LoRA 目前采用的方法是将 $\mathbf{A}$ 初始化为随机高斯分布,将矩阵 $\mathbf{B}$ 初始化为全零矩阵。实际上,不同的初始化策略对模型的性能可能有显著影响,甚至可能对最终结果产生决定性的作用。
- 叠加系数的选择。LoRA 通过将 $\Delta\mathbf{W}$ 乘以一个缩放因子后,再将其叠加到预训练的权重 $\mathbf{W}$ 。这个缩放因子的设定对模型的性能有显著影响,调整它可以显著改变微调过程的结果(目前主流做法是将其设置为 2)。
- 低秩表达的形式。LoRA目前采用的是满秩分解。然而,实际上各种矩阵分解形式均可用于此目的,包括 QR 分解、SVD 分解等。这些不同的分解技术可能会对模型的效果和计算效率产生不同的影响。
- ……
不过目前也有很多研究在解决上述问题,比如:
- PISSA,MiLoRA,LoRA-GA,LoRA-Pro 等等
- RsLoRA,LoRA+ 等等
- AdaLoRA,FLoRA 等等
当然这并不是我眼下关注的重点。我们这里重点关注LoRA的两个消融实验。
低秩流形的重参数化
在 LoRA 中,作者将 $\Delta\mathbf{W}$ 设置为低秩矩阵。这并不是一个一拍脑门子或者想当然的决定,而是有一定的依据。
一些研究表明,在微调阶段,真正有效的是对一个低维流形的重参数化。这意味着模型微调的成功很大程度上依赖于在较低维度上有效捕捉和调整预训练参数,从而适应新的任务需求。
因此,LoRA 才能认为权重的变化可以用一个低秩的矩阵去表示(不过实际上我觉得真正的权重变化应该是满秩的,只不过重要的变化可能集中在一个低秩的流形上)。
弄明白了这一点,自然就明白了 LoRA 在 Sec.7.2 中的实验:
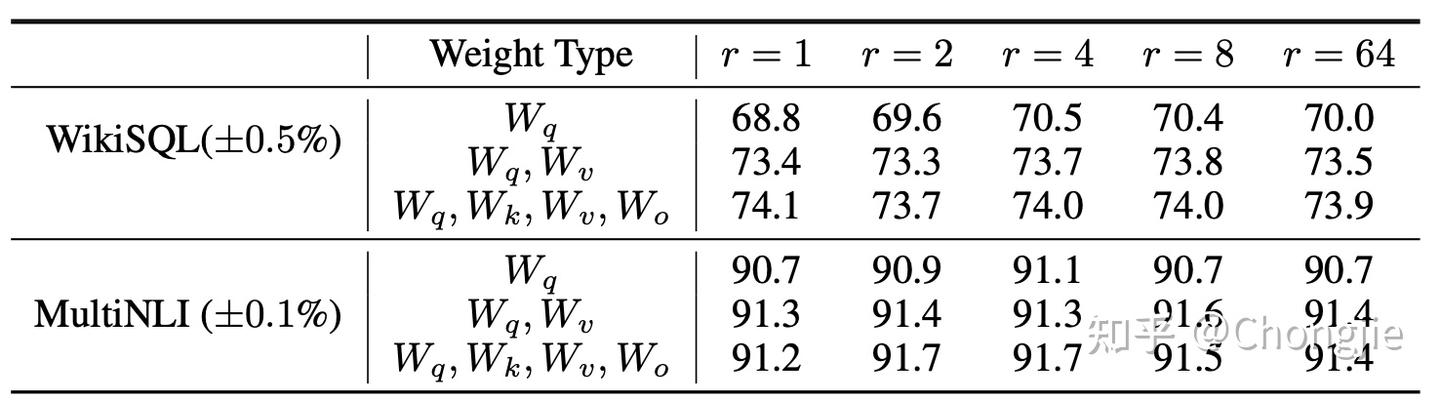
从表中我们可以观察到,LoRA即使在非常小的秩 $r$ 的情况下已经能够表现出与较大秩相媲美的竞争力。这表明将 $\Delta\mathbf{W}$ 设置为低秩矩阵是合理的,好像也验证了“真正有效的是对一个低维流形的重参数化”这一观点。
然而,这自然引发了一个问题:为什么更高的秩的效果反而会不如较低的秩呢?
为了探究这一现象,LoRA 检查了不同的秩的选择下学习到的子空间的重叠情况,结果如图所示:
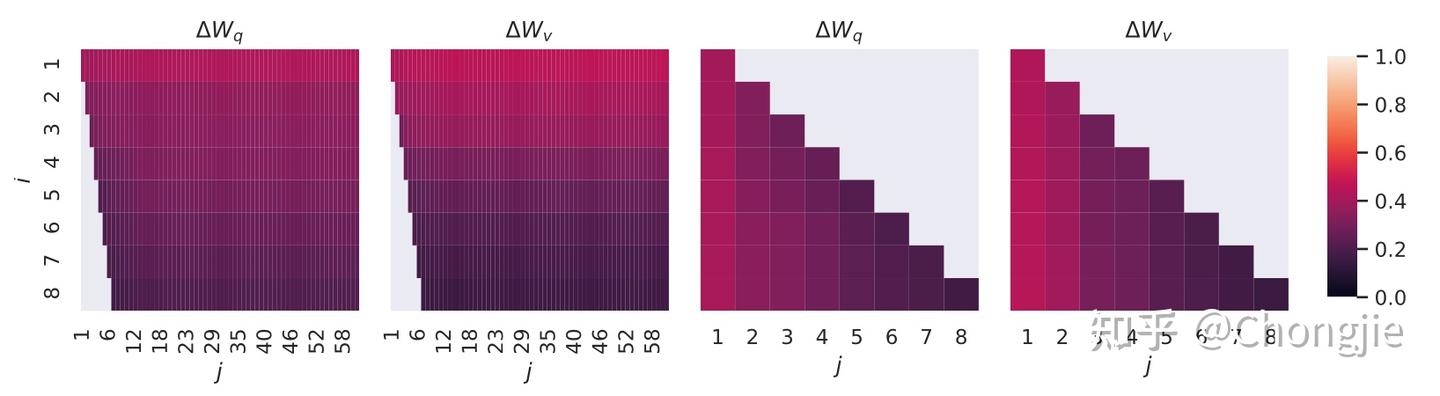
这张图大概意思是说,不同秩设置下的 $\Delta\mathbf{W}$ 的 top 奇异向量方向会有很大的重叠。这指出这些方向是最具有价值的,而其他方向可能主要包含了随机噪声的积累。这也解释了为什么较高的秩设置效果会变差:因为所学习的方向中包含了更多的噪声,一个更大的 rank 并不会覆盖到更多有用的子空间。
权重的变化和预训练权重的关系
那么 $\Delta\mathbf{W}$ 和 $\mathbf{W}$ 有关系吗?
LoRA 里有这么一组实验:它将 $\mathbf{W}$ 投影到由 $\Delta\mathbf{W}$ 的 top 奇异向量所张成的空间上,并计算投影之后的 F 范数。此外,他还将 $\mathbf{W}$ 投影到一个随机矩阵以及该 $\mathbf{W}$ 本身 top 奇异向量所张成的空间上,结果如表中所示:

以下是LoRA的分析:
- 和一个随机矩阵相比, $\Delta\mathbf{W}$ 与 $\mathbf{W}$ 之间存在更强的相关性,这表明 $\Delta\mathbf{W}$ 增强了 $\mathbf{W}$ 中已有的一些特征。相较于 $\mathbf{W}$ 的 top 奇异方向, $\Delta\mathbf{W}$ 仅增强了在 $\mathbf{W}$ 中未被强调的方向。此外,这种增强的幅度相当大。这表明, $\Delta\mathbf{W}$ 可能增强了特定下游任务中重要但在预训练中未被强调的方向的特征。
我们重点来看这一部分。首先,通过和 $\mathbf{W}$ 投影到随机矩阵上的F范数相比,投影到另外两个空间上的F范数明显要大得多,这表明 $\Delta\mathbf{W}$ 与 $\mathbf{W}$ 之间存在更强的相关性。其次, $\Delta\mathbf{W}$ 的奇异方向可以理解为是某一下游任务的关键方向。 $\mathbf{W}$ 投影到这个方向的范数表示预训练阶段在这一方向的信息量,因此,用 $\Delta\mathbf{W}$ 信息量的大小除以 $\mathbf{W}$ 的投影,可以得出在这个所谓的“任务相关方向”上放大的倍数。不过这些实验有一个重要的前提,即 F 范数的大小可以表示信息量的多少(这一问题我们在 FLoRA 的工作中做了一些尝试)。我查阅了一些资料,没有找到一篇相关论文,如果各位发现了蛛丝马迹,欢迎多多分享。
其实这一部分LoRA的讨论中,牵扯到很多不明确的定义。比如什么是矩阵的方向?什么叫增强了特征?这也是我在读这一部分过程中比较迷惑的地方。