深入解析LoRA-Dash:释放特定任务方向性能的微调方法
我们于2024年9月2日在Arxiv提交了我们最新的工作:LoRA-Dash
文章链接:
Unleashing the Power of Task-Specific Directions in Parameter Efficient Fine-tuning
代码链接:
项目主页:
目前的LoRA-Dash为初代目,欢迎各位提出宝贵的意见,便于我们后续的修改。
研究动机
top,bottom还是random?
LoRA 已无需多作介绍,作为微调领域家喻户晓的方法之一,其影响广泛。在此前调研相关方法时,我注意到有几篇专门讨论 LoRA 初始化的研究工作:
- PISSA:认为 LoRA 初始化中的矩阵 $\mathbf{A}$ 和 $\mathbf{B}$ 应对应于权重矩阵 $\mathbf{W}$ 的最大奇异值部分。
- MiLoRA:则提出 LoRA 初始化的 $\mathbf{A}$ 和 $\mathbf{B}$ 应反映 $\mathbf{W}$ 的最小奇异值部分。
除此之外,还有一些方法提出应调整权重矩阵W的最大奇异方向,例如 Spectral Adapter,或随机选择奇异方向进行调整,如 RoSA。在每篇相关论文中,作者均声称其方法效果最佳,并通过消融实验证明了应该调整他们所认为的奇异部分。
这就很有趣了。从论文写作的角度来看,作者需要保持逻辑的一致性,确保他们所强调的有用部分在消融实验中得到验证。然而,让人感到困惑的地方在于,这些方法之间不应存在如此大的差异。每个研究的结果似乎都支持不同的奇异方向调整策略,反而加剧了这一问题的复杂性。这进一步表明,如何有效选择和调整奇异方向仍然是一个具有争议且尚未完全解决的关键问题。
既然如此,我们不妨以一个旁观者的角度,简单分析一下哪一部分在 LoRA 初始化中可能更为有用。从直觉上看,top 奇异方向确实包含了预训练过程中模型学到的最有用的信息。而微调的目的正是为了利用这些预训练过程中获得的知识。因此,直接对这些重要的奇异方向进行调整,反而可能破坏这些信息的有效性,导致微调效果不佳。
我个人在实验中也发现了这一点:调整 top 奇异方向通常不会带来显著的性能提升,甚至有时会影响模型的表现。这表明在微调过程中,保留这些方向的结构可能比过度调整它们更为重要。因此,探索其他奇异方向的调整方式可能会是更有效的策略。
那么就把目光集中在随机选择奇异向量微调与bottom奇异向量的微调。从逻辑上讲,我同意 bottom 奇异向量的微调似乎更为合理。首先,bottom 奇异向量通常代表预训练过程中模型学到的较不重要或次要的信息。因此,微调这些向量首先不会干扰模型在预训练时捕获的关键信息。这有助于保留预训练中获得的核心知识。其次,通过微调这些较不重要的部分,我们可以“化无用为有用”,让这些向量在下游任务中发挥作用,捕捉到与特定任务相关的信息。这种策略能够在保持预训练模型核心能力的基础上,利用微调过程为任务添加新的、有针对性的信息。因此,bottom 奇异向量的微调在理论上可能是一种既能保持原有知识,又能引入任务相关调整的有效方式。相较之下,随机选择奇异向量的方法尽管具有探索性,但在实际效果上可能不如 bottom 奇异向量那么稳定和具有针对性。
不过,我隐隐约约记得,上述的这些分析我好像在 LoRA 里见过。
回顾LoRA
在重新阅读 LoRA 的第7节时,我发现了一些可以验证上述分析的内容。例如,LoRA 指出, $\Delta\mathbf{W}$ 的作用在于扩大权重矩阵 $\mathbf{W}$ 中不重要的方向。这进一步证明了在微调过程中,不应选择 top 奇异向量进行调整。同时,LoRA 通过大量实验表明,微调过程中真正被学习的内容是 task-specific directions (TSD),这些方向对下游任务至关重要。因此,我们调整的重点应该是 TSD,而非 top、bottom 或 random 的奇异向量。
然而,LoRA 的结论中关于TSD的描述存在一些矛盾之处。例如,LoRA 一方面认为 TSD 是权重矩阵 $\mathbf{W}$ 的奇异方向,另一方面又将TSD定义为 $\Delta\mathbf{W}$ 的奇异方向。此外,LoRA 还认为 TSD 可能包含一些与任务无关的方向,虽然这一说法看似有些矛盾和滑稽。
这些不一致之处引发了我们的进一步思考。我们认为问题的根源在于对 TSD 的定义不够清晰——实际上,这是对整个框架的基础定义(如矩阵方向等)存在不明确之处。因此,我们决定从头开始重新定义一个更加清晰的框架,作为 TSD 理论的基石,并在此基础上构建完整的 TSD 体系。
从头搭建特定任务方向的框架
TSD的定义
首先,定义矩阵的基、矩阵的方向如下:
- 定义 1:对于一个矩阵 $\mathbf{A}$
,其左奇异向量和右奇异向量分别由矩阵 $\mathbf{U}$
和 $\mathbf{V}$
表示,矩阵 $\mathbf{A}$
的基定义如下:
- 核心基:矩阵 $ \mathbf{A}$ 的核心基定义为 $ \{\mathbf{u}_i \mathbf{v}_i^\top\}$ ,其中每个 $\mathbf{u}_i \mathbf{v}_i^\mathsf{T}$ 是由奇异向量 $\mathbf{u}_i $ 和 $\mathbf{v}_i$ 构成的秩为 1 的矩阵。
- 全局基:矩阵 $\mathbf{A}$ 的全局基定义为 $ \{\mathbf{u}_i \mathbf{v}_j^\mathsf{T}\}$ 。对于所有 $ i,j$ ,涵盖了左奇异向量和右奇异向量的所有组合。
- 定义 2:矩阵 $\mathbf{A} \in \mathbb{R}^{n \times m}$ (其中 $ n < m $ )的方向基于其全局基定义,采用其奇异值 $\mathbf{\Sigma} $ 的扩展集合,并用零填充,具体表示为 $ (\sigma_1, 0, …, 0, \sigma_2, 0, …, 0, \sigma_n, …, 0) \in \mathbb{R}^{nm} $ ,即通过行展平的 $\mathbf{\Sigma}$ 。
注意到任何全局基都可以视为一个单位方向,因为它的方向是一个 one-hot 的向量。因此,我们也称核心(全局)基为核心(全局)方向。
我们知道对于任何特定任务,矩阵空间 $\mathbb{R}^{n\times m}$ 中存在一个最优矩阵 $\mathbf{W}^*$ 。对于预训练权重矩阵 $\mathbf{W}$ ,其针对该任务的最佳调整为 $\Delta \mathbf{W}^* = \mathbf{W}^* - \mathbf{W}$ 。在PEFT中,我们只能获得 $\mathbf{W}$ 及其方向的信息。由于 $\Delta\mathbf{W}^*$ 和 $\mathbf{W}^*$ 的方向基于各自的基,我们首先将二者投影到 $\mathbf{W}$ 的全局基上。
- 定义 3:定义 $\mathbf{\Pi}(\cdot)$ 为将一个坐标系中的方向投影到另一个坐标系中的投影算子。特别地, $\mathbf{\Pi}_\mathbf{W}(\mathbf{A})=(p_{11}, \dots, p_{nm})\in\mathbb{R}^{nm}$ 是将矩阵 $\mathbf{A} \in \mathbb{R}^{n \times m}$ 的方向投影到矩阵 $\mathbf{W} \in \mathbb{R}^{n \times m}$ 的全局基上。
基于矩阵 $\mathbf{W}$ 的全局基, $\mathbf{\Pi}_\mathbf{W}(\mathbf{W}^*)$ 表示 $\mathbf{W}$ 需要演变的方向。由于 $\mathbf{W}$ 最多只能利用 $n$ 个核心基,它只能改变其方向的 $n$ 个值。因此,重点关注核心方向的变化。
变换过程中,不同核心方向的坐标值变化程度不同,受下游任务的多样性影响,某些核心方向可能变化显著,而其他方向变化较小。定义的变化率 $\delta_i$ 衡量了第 $i$ 个核心方向的变化程度:
$$ \delta_i = |\frac{\mathbf{\Pi}_\mathbf{W}(\mathbf{W}^*)_{ii} - \sigma_i}{\sigma_i+\epsilon}| = |\frac{\mathbf{u}_i^\mathsf{T}\mathbf{W}^*\mathbf{v}_i - \mathbf{u}_i^\mathsf{T}\mathbf{W}\mathbf{v}_i}{\sigma_i+\epsilon}|=|\frac{\mathbf{u}_i^\mathsf{T}\Delta\mathbf{W}^*\mathbf{v}_i}{\sigma_i+\epsilon}| = | \frac{\mathbf{\Pi}_\mathbf{W}(\Delta\mathbf{W}^*)_{ii}}{\sigma_i+\epsilon}|. $$因此,我们可以定义 TSD 为:
- TSD 定义:对于某个特定任务和预训练权重矩阵 $\mathbf{W}$ ,假设该任务的最优权重为 $\mathbf{W}^*$ ,则该任务在 $\mathbf{W}$ 上的任务特定方向(TSD)是指那些在从 $\mathbf{W}$ 到 $\mathbf{W}^*$ 的变化过程中,其坐标值表现出显著高变化率 $\delta$ 的核心方向。
通过 TSD 的定义,我们可以很直接的得出以下结论:
TSD 是预训练权重 $\mathbf{W}$ 的核心方向子集。它们与每个任务相关,意味着在不同任务中,TSD 是不同的,但对于某一特定任务来说,它们是固定的。 与较大奇异值关联的核心方向不太可能被识别为 TSD,因为它们的坐标变化率通常比与较小奇异值关联的方向更小。
有了 TSD 的定义,我们接着再来探索 TSD 的性质。
TSD的性质
我们假设通过全量微调可以获得最优权重为 $\mathbf{W}^*$ ,通过在常识推理任务上全量微调 LLaMA-7B,我们最终计算得到每个方向的变化率,结果如图所示:
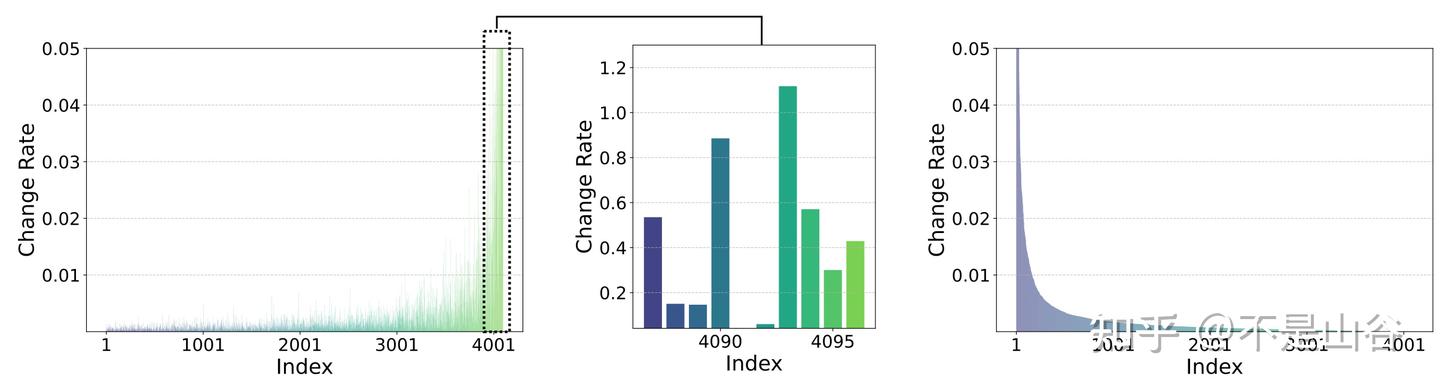
首先,图的左侧展示了每个方向的变化率,横坐标为奇异值的索引,随着索引增大,奇异值减小。从图中可以明显看到,变化率较大的方向大多集中在较小的奇异值索引位置。然而,中间的图表明,奇异值越小并不总是伴随着更大的变化率,说明变化率与奇异值的大小并非简单的线性关系。最右侧的图对所有方向的变化率进行了从大到小的排序,清晰显示出 TSD 仅占据极少数方向,大多数方向的变化率非常小。这表明在微调过程中,只有极少数方向真正对任务产生显著影响,而大部分方向的变化率几乎可以忽略不计。因此,我们可以得出 TSD 的两个性质:
- TSD 主要对应于 $\mathbf{W}$ 较小但非最小的奇异值相关的核心方向。
- TSD 仅涵盖少数方向,这些方向在从 $\mathbf{W}$ 到 $\mathbf{W}^*$ 的转变过程中具有显著的变化率,而其他大多数核心方向的变化率则较小或可以忽略不计。
还有一件事,TSD 是真的任务相关吗?
为此,我们采用了一个典型的例子:以主体驱动的生成任务为研究对象。在此设置中,我们跟踪了不同主体作为目标时所捕捉的 TSD,并分析了这些 TSD 之间的关系。
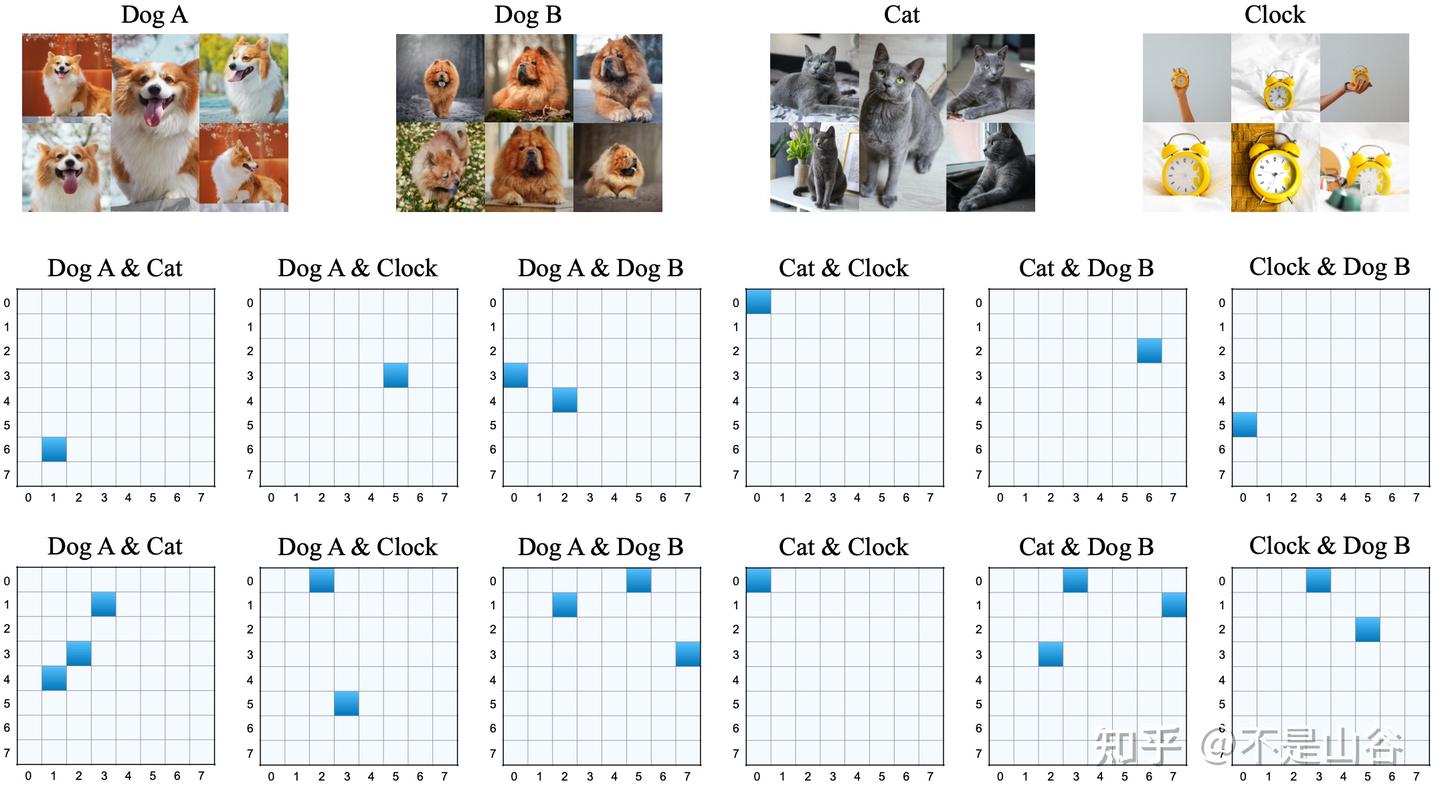
这张图的第一行显示了不同主体的图像。第二行和第三行展示了从 U-net 模型中两个不同层提取的结果。每个子图展示了两个不同主体捕捉到的TSD的相似性。每个子图的标题表明了对应的主体,图中第一主体的方向顺序由列表示,第二主体的方向顺序由行表示。深蓝色区域突出显示了两个主体的方向相重合的部分。
实验结果证实了 TSD 的任务特异性;每个任务都表现出不同的 TSD,任务之间的重叠极少。此外,即使任务共享相同的方向,这些方向的重要性在不同任务中也存在显著差异。例如,如第二行第一张子图所示,“Dog A” 和 “Cat” 共享一个共同方向,但对于 “Dog A” 来说,该方向的重要性排名第七,而对于 “Cat” 则排名第二。更进一步,关系密切的任务往往共享更多的方向,如 “Dog A” 和 “Dog B”之间的情况;然而,这些共享方向在每个任务中的重要性仍然有所不同。该差异性进一步强调了 TSD 的任务特异性,展示了它们在不同情境下的独特性和可变影响。
使用TSD的挑战
尽管我们已经深入探讨了 TSD 的定义和特性,但一个重大挑战在于,在微调之前, $\Delta\mathbf{W}^*$ 和 $\mathbf{W}^*$ 均是未知的,这意味着在实际的微调场景中提前利用 TSD 信息几乎是不可能的。
尽管面临这一明显的挑战,我们并未因此止步,而是将希望寄托于 $\Delta\mathbf{W}$ 。我们假设,LoRA 预测的 $\Delta\mathbf{W}$ 中变化率最高的核心方向与 TSD 密切相关。为了验证这一假设,我们进行了两类实验。首先,我们想知道基于 $\Delta\mathbf{W}$ 预测的(前 8 个)方向有没有包含 TSD 中变化率最大的(前 4 个)方向,我们把这一指标叫做recall; 我们还想知道,基于 $\Delta\mathbf{W}$ 预测的(前 8 个)方向是不是都落在 TSD 中变化率最大的(前 16 个)方向中,我们把这种指标叫做accuracy。实验结果如下图所示:
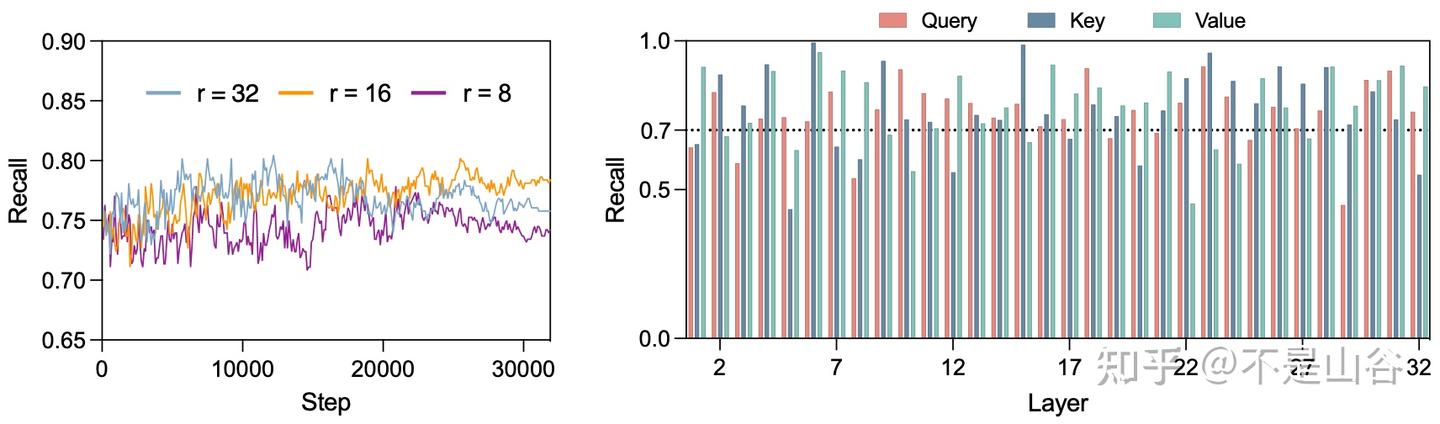
以 accuracy 为例:我们在 LoRA 微调过程中,每隔 100 个训练步骤跟踪 LLaMA-7B 模型中 query、key 和 value 层的预测方向的准确率,分析持续更新的 $\Delta\mathbf{W}$ 捕捉 TSD 的能力。左图展示了在所有 query、key 和 value 层的平均准确率,显示出模型在每个训练步骤中保持任务特定知识的能力。在不同的 LoRA 秩设定下,这些准确率始终超过 0.75,表明 $\Delta\mathbf{W}$ 能够可靠地捕捉并整合 TSD 信息。右图针对秩设定为 $日2$ 的情况,计算了各 query、key 和 value 层在所有训练步骤中的平均准确率,揭示了它们对 TSD 的敏感性。大多数层的平均准确率保持在0.75以上,显示了其捕捉 TSD 信息的鲁棒性。
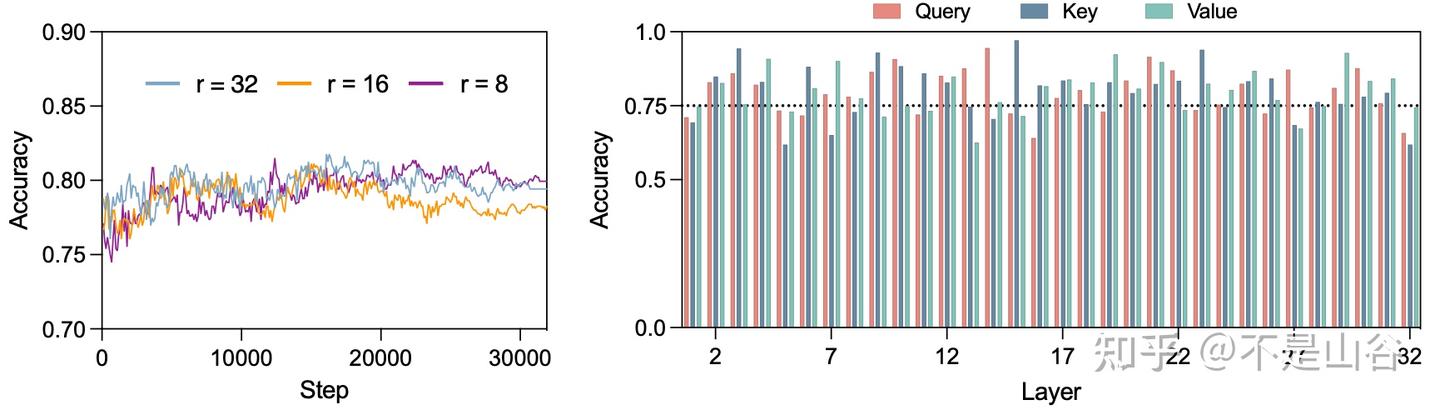
这表明 $\Delta\mathbf{W}$ 不仅能够捕捉到TSD中变化率最大的部分,而且其捕捉到的方向整体上也处于 TSD 变化率最大的前列。这得出了一个重要结论:
- 无论 LoRA 的秩设置、训练步骤,还是模型中的特定层,LoRA 的 $\Delta\mathbf{W}$ 始终能够捕捉任务特定方向(TSD)的信息。
这一结论令人振奋,表明即使在没有TSD先验知识的情况下,我们仍然可以通过LoRA训练过程中获得的 $\Delta\mathbf{W}$ 捕捉到这些关键的任务特定信息。
LoRA-Dash:进一步释放TSD的潜力
为了加速在TSD方向上的学习效率,减轻 $\Delta\mathbf{W}$ 的学习负担,我们提出了一种新方法——LoRA-Dash。该方法旨在更高效地捕捉任务特定方向,从而提升微调过程的速度与效果。
LoRA-Dash 包含两个主要阶段:- “预启动阶段”:在此阶段,TSD 被识别,这是模型优化的关键部分,确保找出最需要调整的方向。具体而言,LoRA-Dash 在经过 $t$ 次更新后利用得到的 $\Delta\mathbf{W}$ 进行 TSD 的预测,确定下一阶段需要优化的方向。
- “冲刺阶段”:在这一阶段,模型充分利用之前识别出的 TSD 进行微调优化,使预训练模型更好地适应特定任务。具体来说,LoRA-Dash 直接模拟 TSD 的坐标变化,加速模型在新任务中的适应性调整,从而显著提升其表现。
LoRA-Dash的伪代码为:

实验
我们在常识推理(commonsense reasoning)、自然语言理解(natural language understanding)和主体驱动生成(subject-driven generation)任务上做了实验。 实验结果表明,LoRA-Dash 在各个任务上都取得了远超 LoRA 的性能提升。实验结果证明了 TSD 对于下游任务的有效性,LoRA-Dash 充分释放了 TSD 的潜能,进一步激发了高效微调的性能水平。
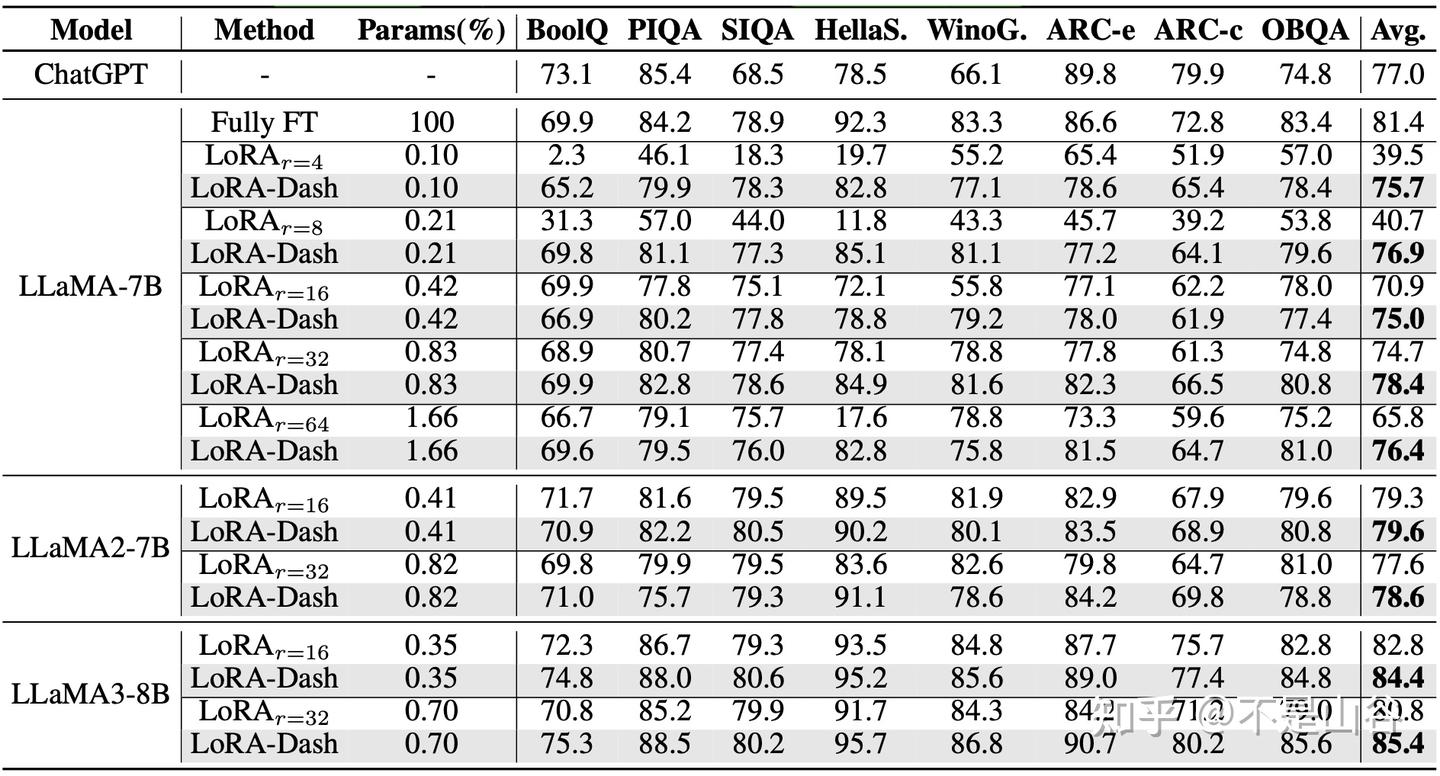
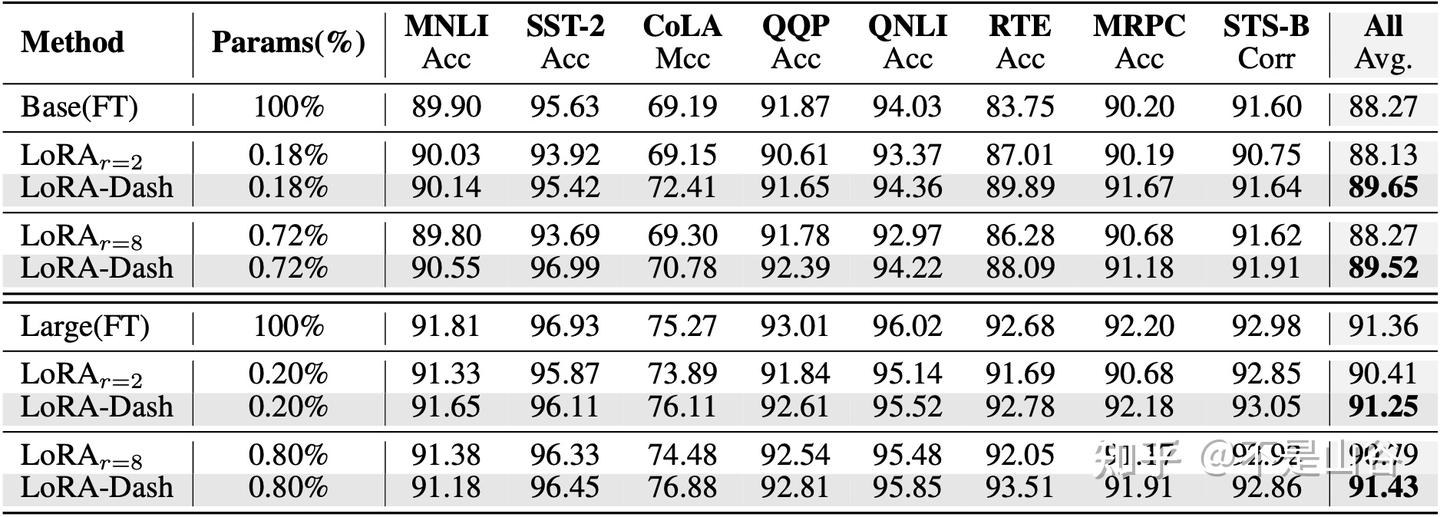

我们也做了一系列的实验。首先,我们探讨了预启动阶段确定的方向,冲刺阶段后的最终方向与 TSD 的关系,目的是确定 LoRA-Dash 是否能够放大TSD的信息,以及如果能够放大,这种放大的程度如何。接着,我们比较了不同方向(如奇异值最大或最小的方向)的有效性,并分析了预启动阶段的长度和冲刺阶段方向数量对性能的影响。最后,我们验证了TSD中的信息是否能够提升其他方法的性能。更多详细内容欢迎参阅原文。